#Technomous

从 8 和 9 说起

看到题目，你也许会问：8 和 9，两个普通的数字，又有什么可说的呢？但在数学家眼中，这两个数字可不寻常：9 比 8 大 1，8 是一个立方数，它是 2 的立方，而 9 是一个平方数，它是 3 的平方。8 和 9，就是一个立方数紧紧挨着平方数的例子。那么，数学家自然会问：还有没有别的立方数，它紧紧挨着一个平方数呢？

或者用数学的语言来说，$x^2-y^3=1$ 这个方程，除了 $x=3,y=2$ 之外，还有别的正整数解吗？

我们先在直觉上探索一下，平方数和立方数，当它们越变越大的时候，在所有正整数当中也会越来越稀疏。就像两个越来越不喜欢出外的人，即使是邻居，也许一开始会打个照面，但之后出门的次数越来越少，也就越来越不可能碰上面。数学家们甚至猜测，即使不限定于平方数和立方数，就算是任意大于 1 的次方数，它们“碰面”也只有 8 和 9 这一回。用严谨的数学语言来说，就是方程
$x^a-y^b=1$，在 a 和 b 大于 1 的条件下，只有一组解，就是 $x=3,a=2,y=2,b=3$。这又被称为卡特兰猜想（Catalan’s conjecture）。

直觉上，卡特兰猜想应该是对的，但直觉毕竟是直觉，它不是数学证明。虽然平方数和立方数它们越来越稀疏，但是正整数有无限多个，它们有无数次碰面的机会，谁知道它们会不会在通向无限地平线的路途中就抓住了又一次机会呢？所以，我们需要数学证明，只有数学证明，才能从逻辑上根本地否决这种可能性。

我们来看看数学家是怎么思考的。

数学家们想要的是一个数学证明。我们重新考虑方程 $x^a-y^b=1$。在这个方程里什么东西最麻烦呢？减法很简单，等于号很简单，剩下的就是乘幂操作了。那么，有什么办法能去掉乘幂这个麻烦事呢？这个办法就是对数，大家在中学都学过。对数能将乘幂转化为更简单的乘法：$\ln (x^a)=a\ln (x)$。我们先将方程改写成 $x^a=y^b+1$，然后两边取对数，就得到了 $a\ln (x)=\ln (y^b+1)$。

现在，方程里最麻烦的又是什么呢？就是对数里边的加法，因为对数和乘法很友好，但跟加法实在谈不来，$\ln (x+y)$ 并没有一个好的表达式。有什么方法可以绕过去呢？我们想到，$y^b$ 是一个次方数，它可以非常大，要多大有多大，而相比之下，加上去的这个 1 非常小非常小，小得几乎可以忽略不计。而对数函数增长得又非常慢非常慢，$\ln (20)$ 大概是 3，$ln(400)$ 大概是 6，要想对数值增加 3，原来的数要增加 20 倍，要等到 ${10}^{13}$，也就是万亿，对数值才达到 30。而对于一万亿来说，这个小小的 1 实在是零头中的零头。

对数函数的增长，由方弦制作

但数学是严谨的，虽然这个 1 很小，带来的影响更小，但我们不能直接说可以把 1 去掉。但这难不倒数学家：既然不是直接相等，划个界限总可以吧？用一点简单的高等数学，我们可以得到如下的不等式：

也就是说，去掉 1 和不去掉 1，对于对数值的影响只有 $y^{-}b$，$y^b$ 的倒数。因为 $y^b$ 可以非常大，它的倒数也就非常小。如果它增长十倍，它的倒数就会变成原来的十分之一。我们刚才说到，$y^b$ 要达到万亿，它的对数值达到 30，这时候它的倒数，也就是加 1 造成的误差，只有万亿分之一。这是个什么概念呢？相当于在测量地球到太阳的距离时，不小心多加了根头发丝。在现实世界中，即使多么严谨的测量，这种程度的误差可能也就放过去了。但在数学中，无论多小的误差，不应该舍弃的时候就不能舍弃。

将这个误差的结论代入原来的方程，我们得到：

也就是说，我们要寻找两个正整数，它们的对数值的某个倍数非常接近。这就需要对正整数的对数进行深入的研究。在 1966 年到 1967 年，数学家阿兰·贝克（Alan Baker）写出了一系列的文章，其中给出了正整数乃至所谓“代数数”（也就是多项式方程的解），它们的对数的倍数之间距离的一个下界。也就是说，上面的不等式左边其实不会太小，它会大于某一个关于 $a,b,x,y$ 的函数，可以写成：

那么，如果我们能证明对于绝大部分的 $x,y,a,b$ 都有 $C(x,y,a,b)>y^{-b}$，那么两个不等式就会产生矛盾，方程也就不可能有整数解，这不就解决了卡塔兰猜想了吗？

阿兰·贝克，图片来自上沃尔法赫数学研究所（Mathematisches Forschungsinstitut Oberwolfach）

当然，实际上这种简单粗暴的方法并不能解决问题。$C(x,y,a,b)$ 这个函数，虽然可以明确计算出来，然而得出的函数太小，不足以解决问题。但引出矛盾的方法不只一种。为了证明这类型的结论，贝克发明了一种方法，可以在不同的角度上引出矛盾。而另一位数学家 Tijdeman 利用贝克的方法，找到了一个巧妙的角度，证明了当 $a$ 和 $b$ 足够大的时候，方程必定没有解。而此前人们已经证明了，当 $a$ 和 $b$ 固定的时候，关于 $x$ 和 $y$ 的方程最多只有有限个解，而且给出了这些解的一个上界。结合两个结果，数学家们证明了，整个关于 $a,b,x,y$ 的方程最多只有有限个解。现在在波尔多大学的数学家米歇尔·朗之万（Michel Langevin）计算出了一个明确的上界：$e^{x^{730}}$

也就是说，只要检查比这个数小的所有正整数，如果没有找到别的解，那么就说明 8 和 9 是唯一一对靠在一起的次方数。但这个任务看起来容易，做起来却是无计可施。$e^{x^{730}}$ 有多大？在现实中，能与其相比的数字根本不存在，即使是 1 后面添上宇宙里所有的原子当作 0，这样得到的无量大数，还是连零头的零头都赶不上。对于这么大的数字，表达它都有困难，更何况检查！

数目远超银河中原子个数，图片来自 Wikipedia

你可能觉得，这样找正整数的对数之间的关系，又有什么用呢？好不容易得出一个结果，却只是“原则上可以验证”，根本不能实际计算，这种方法又有什么用？但不要忘记，方法之所以是方法，就是因为它能应用到许多问题上。贝克的这套方法，可以应用到所谓的“丢番图方程”，也就是系数和解都是正整数的方程。大家耳熟能详的费马大定理，可能大家不太熟悉的完美长方体问题，都是悬而未决的丢番图方程。而对这类方程的研究，涉及数论的方方面面。贝克的方法给丢番图方程地研究带来了全新的工具，他也因此获得了 1970 年的菲尔兹奖，那时离他发表相关论文还不到四年。

但卡特兰猜想仍然悬而未决。要等到 2002 年，罗马尼亚的数学家 Preda Mihăilescu 才最终证明了卡特兰猜想。他的方法大量用到了分圆域与伽罗华模的知识，这些都是代数数论中的艰深概念，哪怕是稍稍涉猎，恐怕也需要本文十倍以上的篇幅才能讲个大概。但无论如何，我们现在终于可以确定，8 和 9 在自然数中的确是绝无仅有的一对，在无限的可能中，唯一一对能紧靠在一起的次方数。

卡特兰猜想还有别的变体，比如说人们猜想，对于任意的正整数 $k$，间距为 $k$ 的次方数对只有有限个。对这些变体的探索也非常引人入胜。

但这不是这篇文章的主题。

从整数到多项式

我们在中学里就学过多项式。对于一个变量 $x$，我们取它的一些次方 $x^a,x^b$ 等等，乘上系数，然后加起来，就得到了一个多项式，比如说 $x^7+6x^3+4$ ，就是一个关于 $x$ 的多项式。在这里，我们考虑那些系数都是复数的多项式，也就是复系数多项式。

数学家们很早就发现，这些多项式与正整数有一种神奇的相似性：可以做加法、减法、乘法，也可以分解因数，可以求最大公约数和最小公倍数，同样有着唯一分解定理：正整数可以唯一分解成素数的乘积，而多项式也能唯一分解成所谓“不可约多项式”的乘积。基本上，在数论中对正整数性质的研究，很多都可以直接搬到多项式上来。于是，遇上有关正整数的问题，把它迁移到多项式之中，未尝不是一个提出问题的好办法。自然，因为多项式本来结构就比较复杂，相关的问题也更难解决，但这不妨碍数学家的步伐，毕竟他们要攻克的就是难题。

注：更准确地说，因为正整数和多项式都组成了所谓的“欧几里德整环”（Eucliean domain），所以它们共享非常多的数论性质，比如说，它们都是所谓的“主理想整环”，它们的所有理想都是主理想，也就是某个元素的倍数组成的理想。

此处插播一则笑话：为什么 QQ 只有 QQ 群？因为 QQ 没有理想……

在 1965 年，Birch、Chowla、Hall 和 Schinzel 问了一个问题：如果有两个多项式 $P$ 和 $Q$，它们是互质的，那么 $P$ 的平方和 $Q$ 的立方之间的差距，也就是说 $P^2-Q^3$，可以有多小？这个问题很显然是卡塔兰猜想的延伸。卡塔兰猜想最原始的版本问的是，除了 8 和 9 以外，平方数和立方数的距离能不能达到 1。而 Birch 等人现在问的是，多项式平方和立方的距离最小能达到多少？

当然，要回答这个问题，首先要想办法衡量多项式的大小。对于不同的多项式 $P(x)$，当 $x$ 趋向于正无穷时，$P(x)$ 趋向无穷的速度各有千秋，而决定这个速度的主要因素，就是多项式的次数，也就是多项式中 $x$ 的最高次方是多少。所以，我们选择多项式的次数作为衡量多项式大小的标尺。现在，我们可以用更严谨的方式叙述那四位数学家的问题：

对于某个正整数 $k$，假设有两个互质的多项式 $P,Q$，其中 $P$ 的次数是 $3k$，$Q$ 的次数是 $2k$。那么，多项式 $R=P^2-Q^3$ 的次数最小可以有多小？

我们能看出来，在这个问题中 $P$ 和 $Q$ 的次数不是随便选取的。如果 $P$ 的平方和 $Q$ 的立方次数不一样的话，那么 $R$ 就跟 $P,Q$ 一样大。只有上面的选择方法，才能至少使两者的最高次项互相抵消，使问题变得不那么无聊。另外，对于任何一个例子，我们只要将所有多项式都乘上一个合适的常数，就能得到另一个本质上相同的例子。所以，我们只考虑本质上不同的那些例子。

在论文中，四位数学家给出了一个 $k=5$ 的例子：

在这个例子里，$P,Q,R$ 的次数分别是 15、10 和 6。虽然 $P^2$ 和 $Q^3$ 的次数都是 30，但是它们凑巧在前 24 项的系数都相同，而它们的差仅仅只是一个六次多项式，真是一个难得的巧合。但数学家总是有些贪心，面对这个例子，他们想的是：能不能把 $R$ 的次数再压低一点？能不能找到差距更小的平方多项式和立方多项式？这个想法非常自然，但在反反复复的尝试中，似乎找不到次数更低的例子了。于是，这四位数学家就猜想：这个例子是不是已经无法改进了呢？他们提出了这样的猜想：

对于两个互质的多项式 $P,Q$，假设其中 $P$ 的次数是 $3k$，$Q$ 的次数是 $2k$。那么，多项式 $R = P

• Q ^ 3$ 的次数至少也有 $k+1$，而且总能找到使 $R$ 的次数恰好是 $k+1$ 的例子，也就是说这个下界是紧的。

在刚才的例子中 $k=5$，而 $R$ 的次数恰好就是 5 + 1 = 6，符合猜想。数学家们想寻找更多的这样达到最小差距的例子，尝试在其中寻找规律。但出人意料的是，$k=5$ 的第二个例子，要到 35 年之后的 2000 年，才被 Elkies 发现，而且这个例子的复杂度远远超出了预期。在上面的例子中，我们看到的系数都是相对简单的分数。而现在，请看 Elkies 的这个例子：

在这个新例子中，多项式的系数大大膨胀了，这就解释了为什么寻找第二个例子花了这么长的时间。我们也能从另一个侧面窥见这个问题的难度。比方说，我们希望用待定系数法寻找例子：先将多项式 $P,Q$ 的系数都设为未知数（最高次的系数设为 1），然后计算 $R$ 的所有系数，它们都是之前未知数的多项式。在 $k=5$ 的情况下，我们要求 $R$ 从 $x^{29}$ 到 $x^7$ 的这 23 个系数都是 0，这样就得到了 23 个方程。将它们联立起来，就得到了一个关于 25 个变量的 23 个方程组成的高次方程组，理论上只需要解出这个方程组，就能得到所有的例子。但问题是，这个方程组的总次数是6198727824，大约是六十亿！这样的方程，不要说是人脑，就是计算机也几乎无法解开。但至少，我们知道这些系数都是所谓的“代数数”，也就是代数方程的解。这样庞大而困难的问题，难免令人望而却步。寻找新的例子已经如此困难，更不要说穷尽所有例子了。

但有一帮数学家，光是看了看问题，在餐巾纸上随手涂鸦了一下，就拍着胸脯宣称：$k=5$ 的情况一共就只有 4 个例子，还有两个就继续找吧；不光这样，对于任意 $k$ 的情况，我们都能证明你们的猜想是对的，而且还能帮你们计算所有本质上不一样的例子一共有多少个。

这是什么魔法？

球面覆盖

我们每天睡觉亲密接触的被褥，它的卫生状况值得重视，偶尔就要把被套拆下来洗一洗，洗完再套上去。但这不是个顺当的活计，尽管有系绳，但固定还是相当困难，手艺不好的，实在是难以把它弄得服服帖帖，总是会有些褶皱。这时候难免萌生出偷懒的想法，懒得把被套拉链拉开然后把内芯塞进去了，就随便用被套把内芯当粽子捆了，反正严格来说，的确也是用被套把内芯“套住了”，被套也完成了自身的责任：把内芯的每一处都“挡住”，不让睡觉的人把内芯弄脏。可惜被套一般没有弹性不能延伸，包起来的“粽子”实用面积实在太小，否则这也不失为一个好办法。

无论是正常的还是包粽子的方法，我们都可以说，被套把内芯“覆盖”了。最完美的当然是从头到尾平整光滑的覆盖，内芯上每个地方都被一层被套覆盖；稍差一些，有点皱褶的话，皱褶的地方就会有至少三层被套覆盖着内芯的同一个地方，而且还会有一些“分支点”，皱褶在这些点上开始，又在这些点上终结。如果是包粽子的话，那就不好说了，不过可以肯定的是，内芯上每个点至少有两层被套覆盖。

覆盖的折痕，来自 Wikipedia

在数学家眼中，被套可以看成一个球面：假设被套有弹性，那么在里边装一个气球，再把气球吹起来，被套自然会鼓起来变成球面。同样，内芯也可以看成一个球面。如果我们先在内芯放一个气球，然后把内芯和覆盖它的被套缝起来，不让它们移位，最后将气球吹起来，那么我们就得到了被套这个球面对内芯这个球面的一个覆盖。这样的覆盖变化多端，可以是平滑的，也可以有皱褶，在每一点处，覆盖可以是单薄的，也可以是多重的。

把这些直观印象翻译成数学概念，这是数学家们的拿手好戏。球面之间的覆盖，用数学术语来说，就是从一个球面（被套）到另一个球面（内芯）的连续满射函数 $f$，如果 $x$ 是被套上的一点，那么 $f(x)$ 就是内芯上被 $x$ 这一点覆盖的点。我们要求函数是连续的，因为我们不想把被套扯坏，所以要求被套上的一小块“保护”的也是内芯上的一小块，而不是“分隔异地”的两块；我们要求函数是满射，因为我们希望保护内芯不被弄脏，所以要求内芯上的每一点都有被套保护。当然，数学毕竟是数学，比现实要更天马行空一些。现实中的被套不能穿过自身，而数学中的覆盖则可以。正因为如此，在数学中我们可以把覆盖的皱褶“抚平”，只留下一个个孤立的分支点，这在现实中是不可能的。而我们要求除了分支点以外，球面上的其他点被覆盖的次数都相同，这个次数又被称为球面覆盖的次数。

视频原作者：Dugan Hammock，他的 Youtube频道上有更多关于曲面的精美视频。

然而，这些东西跟多项式又有什么关系呢？

对于数学家来说，关系非常大。因为他们知道，复数组成的复平面，差不多就是一个球面。有一种叫“球极平面投影”的方法，可以将复平面转化为只缺一个点的球面。而如果我们将“无穷大”也加到复平面里，就能把球面缺的点补上，得到的就是所谓的“黎曼球面”。而黎曼球面上的有理函数，也就是两个多项式的商，实际上就是一个球面覆盖。通过研究球面覆盖的性质，数学家们就能间接得知对应的有理函数的性质。

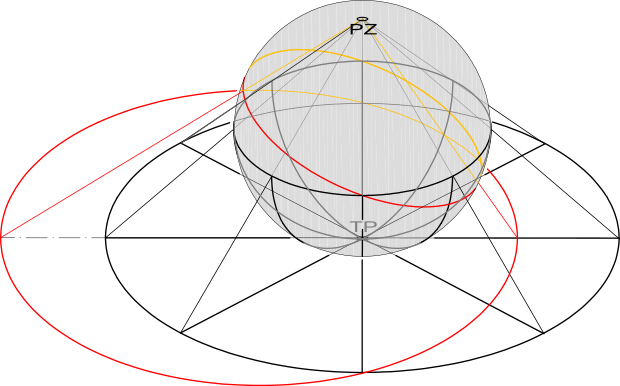
球极平面投影，来自 Wikipedia

我们接下来考虑有理函数给出的球面覆盖。球面覆盖的许多性质都被它的分支点所决定，因为分支点以外的地方都非常平滑，到了乏善可陈的地步，而分支点正是曲面“叠起来”的地方，自然包含了我们想要的性质。我们可以说，球面覆盖的分支点越少，它就越简单。

那么，对于有理函数来说，怎么寻找它的分支点呢？还是拿被套作例子。当被套有皱褶时，皱褶的部分实际上是三层被套覆盖同一点，但同样应该属于皱褶一部分的分支点上，却只有一层被套。也就是说，分支点覆盖的层数比正常的要少一些。如此类推，对于函数 $f(x)$ 引出的球面覆盖来说，假设它的覆盖次数是 $d$ ，那么说某个点 $a$ 是分支点，就相当于说 $f(x)=a$ 这个方程的解值少于 $d$ 个，因为这个方程的每一个解其实都是“被套”上覆盖 $a$ 的一点。换句话说，$a$ 是分支点当且仅$f(x)=a$ 当有重根。

举个实际的例子。我们考虑函数

显然方程

有三次重根 $x=1$，所以 0 是它的一个分支点；而稍微令人意想不到的是，如果我们将它减去 1，就会得到

可以看出来，方程 $f(x)-1=0$ 有两个二次重根，分别是二次方程 $x^2-6x-3$ 的两个解，所以 1 也是一个分支点。最后还有一个分支点比较难想像，那就是无穷远点，因为当 $x$ 趋向无穷或者 0 时，$f(x)$ 也趋向于无穷，所以无穷远点也是一个分支点。可以证明，这个函数再也没有别的分支点了。

最简单的球面覆盖，一个分支点都没有，就是最标准的把内芯塞进被套里的方法。球面到自身的恒等映射 $f(x)=x$ 就是这样的一个例子。可以证明，不存在只有一个分支点的球面覆盖，也就是说，接下来第二简单的情况就是拥有两个分支点的球面覆盖。可以证明，所有拥有两个分支点的球面覆盖，都可以利用适当的变换来“拉扯”变形到 $f(x)$ 是多项式的情况。

数学家们接下来要研究的，自然就是拥有三个分支点的球面覆盖。利用有名的莫比乌斯变换

我们可以将三个分支点分别移动到 0、1 和无穷远点（∞），而莫比乌斯变换不会改变球面覆盖的本质。所以说，我们只需要研究分支点分别在 0、1 和 ∞ 的球面覆盖，而能产生这样的球面覆盖的函数又叫别雷函数（Belyi function，正确地说是球面上的特殊情况），它的名字来源于 20 世纪的俄罗斯数学家别雷（G. V. Belyi）。但实际上，别雷并不是第一个研究别雷函数的人。早在 19 世纪末，大数学家菲利克斯·克莱因（Felix Klein）就已经利用别雷函数构造过一些特殊的球面覆盖（更精确地说，是单值群为有限单群 PSL(2,11) 的球面覆盖，它是一个 11 次覆盖）。

但球面覆盖毕竟太抽象，即使是数学家，不借助适当的工具也难以“脑补”某个具体函数引出的覆盖，而对于一般人来说，光是球面可以穿过自身这一点就足够喝一壶的了，更不要说想像那些“折痕”都集中在几个分支点上的高次覆盖。要研究这些球面覆盖，似乎是难于登天。

但数学家却说，三个分支点的球面覆盖，其实简单得连小朋友都能画出来。

小朋友的涂鸦

要讨论别雷函数，就要对球面覆盖和复分析有些更深入的了解。接下来的内容可能有一点抽象，如果实在不适应，可以跳过，直接看本节最后的结论。

我们要研究的，是分支点分别在 0、1 和 ∞ 的球面覆盖，或者说某个别雷函数 $f(x)$。既然球面覆盖的所有玄妙之处都蕴藏在分支点里，那么肯定要抓住这些分支点来研究。我们之前考虑过一个例子：

它是一个别雷函数，对应着一个球面覆盖。用一点点复分析的知识（代数基本定理），容易知道除去一些特殊情况外，对于任意的常数 $a$，$f(x)=a$ 都有 4 个解。也就是说，这个别雷函数对应着一个次数为 4 的球面覆盖。我们再来看看这个函数的分支点。它在 $f(x)=0$ 处有一个分支点，因为 $x=1$ 是这个方程的三重根，但它还有另一个根 $x=9$，也就是说，0 这个分支点实际上对应两个不同的点：三重根 $x=1$ 和单根 $x=9$。同理，1 这个分支点同样对应两个不同的点，两个都是双重根。我们能看到，两个分支点的分支方式不同，但既然它们从属于同一个球面覆盖，那么之间必然有某种联系。怎么样才能考察它们之间的联系呢？

办法很简单：直接把两个点连起来就好了。也就是说，我们希望观察这两个分支点的每一层覆盖分支之间是如何连接起来的。

更具体地说，因为球面覆盖就是一个球面覆盖着另一个球面，只要在被覆盖的球面上连结 0 和 1 两个点，在得到的线段上涂上极浓重的颜料，等到颜料渗透到覆盖的每一层之后，再将覆盖展开，得到的就是球面上的一幅图。用术语来说，就是研究 $f^{-1}((0,1))$。那么，我们得到的图像会是怎么样的呢？还是用刚才的函数来举例，我们得到的图像如下：

由方弦使用 Maple 制作

在上图中，黑点代表 0 对应的点$x=1$ 和 $x=9$，而白点代表 1 对应的点 $x=3+2\sqrt{3}$ 和 $x=3-2\sqrt{3}$。因为这个球面覆盖的次数是 4，所以线段 [0,1] 上的点实际上被覆盖了四次，也就是说，当覆盖展开之后，我们将会看到四段曲线（四条边），它们连接着 0 对应的两个点 $x=1$ 和 $x=9$，还有 1 对应的两个点 $x=3+2\sqrt{3}$ 和 $x=3-2\sqrt{3}$。三重根 $x=1$ 上连着三条边，单根 $x=9$ 只有一条，而两个双重根 $x=3+2\sqrt{3}$ 和 $x=3-2\sqrt{3}$ 各自连接两条边。函数在 $x=0$ 和 $x\to \mathrm{\infty }$ 两个点上发散，而这个图恰好又有两个面，外部的面对应 $x\to \mathrm{\infty }$，而内部的面对应 $x=0$ ，而这些面的度数（也就是边界的长度）与函数在对应点上发散的度数相关。也就是说，单单从这幅图像里，我们就能读出函数本身的许多代数性质。如果把顶点连接的边的数目称为顶点的度数的话，图像性质与代数性质的对应可以归纳成下面的列表：

实际上，对于所有的别雷函数，展开对应的球面覆盖后，线段 [0,1] 的图像总是包含着我们想要的很多代数性质：边的数目对应着覆盖的次数，黑点对应着 $f(x)=0$ 的分支，白点对应着 $f(x)=1$ 的分支，面对应着无穷大的分支，而每一个点和每一个面连接多少条边，都对应着球面覆盖在对应的分支上“折叠”起来的方法。

那么，别雷函数对应的这些图像，到底又是什么呢？

我们先忽略那些点和线的具体位置和形状，而只关注它们是如何在球面上连结起来的。用数学术语来说，就是先忽略它们的几何性质，而专注于它们的组合性质。首先，因为每条边实际上都来自线段[0,1]，所以它们连结的必定是一个对应着 $f(x)=0$ 的黑点和一个对应着 $f(x)=1$的白点。也就是说，别雷函数对应的图像，实际上可以抽象成一个二部图，这类图的顶点，一黑一白，而每条边的两端恰好是一黑一白两个顶点。但这些图像跟一般所说的二部图不完全一样。在数学中，一个图就是一堆顶点加上连结顶点的一些边，但连结同一个顶点的边之间并没有什么特别的关系。但别雷函数对应的图像实际上是一个画在了球面上的图，所以连结同一个顶点的边会在围绕在顶点周围，这就给它们赋予了顺序关系。这样画在了球面（或者别的封闭曲面）上的图，又叫组合地图。而别雷函数对应的图像，正式的名称是平面上的二部地图。在这里，组合地图即使画歪了一点，只要保持顶点、边以及边之间的关系，还算是同一个地图。

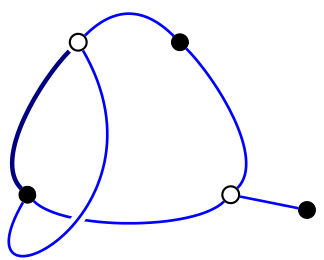
一个亏格为 1 的二部地图，由方弦制作

现在我们知道，每个别雷函数都对应着一个平面上的二部地图，那么是不是所有这样的地图都对应着一个别雷函数呢？事实上，利用一些复分析方面的知识，可以证明别雷函数与球面上的二部地图有着一一对应的关系。不仅如此，我们还能把这些别雷函数限定为系数是代数数的分式（代数数就是整系数多项式方程的解）。这实际上就是别雷的贡献：他在 1979 年证明了，对于一大类重要函数（所谓的“光滑代数曲线”），它们（的适当的等价类）与别雷函数引出的球面覆盖有着一一对应的关系。这些“光滑代数曲线”可以粗略理解为分支点只有0、1 和 $\mathrm{\infty }$，系数是代数数的分式。也就是说，如果我们要找分支点满足某些条件的分式，只需要看看根据这些条件能不能在平面上画出一个二部地图就可以了。

总结一下：三个分支点的球面覆盖，等价于所谓的“平面上的二部地图”，在这个地图上有黑色和白色两种顶点，而每条边都连接一黑一白两个顶点，从而把所有顶点连成一片。而球面覆盖的许多性质，都能反映在地图上的顶点、边和面上。别雷证明了，“光滑代数曲线”（大概就是某一类系数是代数数的分式）与三个分支点的球面覆盖有着一一对应的关系。所以，要寻找分支点满足某些条件的分式，只需要看看能不能画出满足对应条件的二部地图。而任意一个二部地图，哪怕是小朋友的涂鸦作品，也必然存在对应的分式，它的球面覆盖展开之后就是这个二部地图。

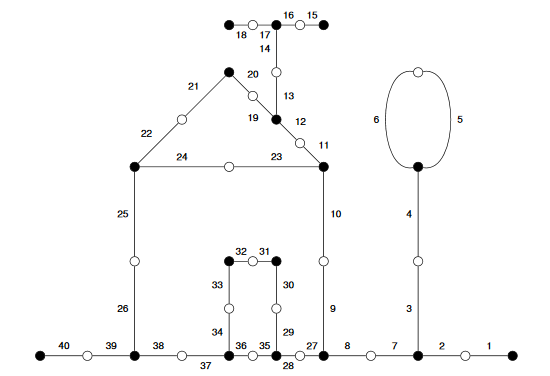
涂鸦的例子，作者为Laurent Bartholdi

说了半天，云里雾里的，这又有什么意义？

地图的魔术

我们先回到一开始的问题：对于某个正整数 $k$，假设有两个互质的多项式 $P(x),Q(x)$，其中 $P(x)$ 的次数是 $3k$，$Q(x)$ 的次数是 $2k$ 。那么，多项式 $R(x)=P(x{)}^2-Q(x{)}^3$ 的次数最小可以有多小？

我们现在用别雷函数、球面覆盖和二部地图的眼光来看这个问题。首先，我们来考虑分式
$f(x)=-\frac{Q(x{)}^3}{R(x)}$。可以证明，如果 $f(x)$ 除了 0、1 和 $\mathrm{\infty }$ 以外还有别的分支点的话，我们就得不到最优解。所以，我们可以假设 $f(x)$ 是别雷函数。

函数 $f(x)$ 在 0 处的分支点就是 $Q(x{)}^3$ 的根，也就是 $Q(x)$ 的根（计算重数的话，一共有 $2k$ 个），但每个根的重数要乘以 3。同样的道理，它在 $\mathrm{\infty }$ 处的分支点就是 $R(x)$ 的根，再加上无穷远点 $x=\mathrm{\infty }$，因为 $R(x)$ 的次数比 $Q(x{)}^3$ 要小，所以当 $x$ 趋向于无穷时，$f(x)$ 也会趋向于无穷。那么，它在 1 处的分支点又怎么样呢？这就是我们选取 $f(x)$ 的目的：$f(x)-1$ 就等于 $-\frac{P(x{)}^2}{R(x)}$，所以，$f(x)$ 在 1 处的分支点，就是 $P(x)$ 的根（计算重数的话，一共有 $3k$ 个），但每个根的重数要乘以 2。我们可以假定 $f(x)$ 没有别的分支点。我们要问的问题实际上就是：$f(x)$ 在 $\mathrm{\infty }$ 处的分支点至少有多少个？

我们重温一下球面覆盖和二部地图概念之间的翻译表。

如果将所有这些要求翻译成二部地图的概念，我们实际上要解决的是这样的一个问题：

如果一个二部地图，它的白色顶点度数都是偶数，并且加起来是 $6k$，而黑色顶点的度数都是 3 的倍数，加起来也是 $6k$，那么，它至少有多少个面？（在这里，我们不能说白色顶点的度数都是 2，因为 $P(x)$ 可能有重根，黑色顶点同理）

如果 $k$ 很小的话，试着画画也就可以了。但因为现在 $k$ 可以要多大有多大，乱试一通大概不太管用。这就是借助别的数学工具的时候了。18 世纪的大数学家欧拉（顺带一提，按博士导师的师承关系的话，他是笔者以及很多人的祖师爷）在开辟图论这一领域时，证明了下面的等式：如果一个平面地图有 $v$ 个顶点、$e$ 条边和 $f$ 个面（最外面的也算一个面）的话，那么必然有 $v-e+f=2$

我们把这个等式套到我们的问题上，看看会得到什么。容易知道，我们的二部地图必定有 $3k$ 条边，也就是说 $e=3k$。把等式改写一下，我们得到 $f=2-v+3$。因为我们想知道至少有多少个面，所以我们应该尝试寻找最大可能的 $v$，也就是最大化顶点的个数。因为白色顶点的度数都是偶数，并且加起来是 $6k$，要获得最多的顶点，最好的方法就是要求每个顶点的度数都是 2，这样就能拿到最多的 $3k$ 个顶点。同理，对于黑色顶点，最好的情况就是每个顶点的度数都是 3，这样能拿到最多的 $2k$ 个顶点。所以，顶点的总数合起来最多是 $5k$ 个，也就是 $v\le 5k$。代入欧拉的等式，得到的就是 $f\ge k+2$，也就是说这样的平面地图至少有 $k+2$ 个面。考虑到其中一个面对应的是无穷远点 $x = $\mathrm{\infty }$$，这就意味着 $R(x)$ 的度数至少是 $k+1$，而且要达到这个度数，$R(x)$ 必须不能有重根，也就是说每个面（除了最外边）的度数都是 2。

我们得到了想要的下界，但还要证明这个下界能够达到，而我们又不想计算无穷个满足条件的多项式，怎么办呢？这就是别雷定理出场的时候了：它告诉我们，只要对应的二部地图能画出来，那么满足要求的分式必定存在，而且系数都是代数数。所以，我们根本不需要计算，只需要画出满足条件的二部地图就足够了。这样的地图画法非常简单：首先画出一棵有 $2k$ 个黑色顶点的三叉树（也就是没有圈的地图，而分叉的顶点度数都是 3），在每个叶顶点（也就是度数为 1 的顶点）上画一条跟自身连接的边，然后在每条边中间插入一个白色顶点，就得到了满足条件的二部地图。可以证明，满足条件的二部地图必定能用这样的方法构造出来。根据别雷定理，既然二部地图能画出来，那么满足要求的分式存在，也就是说使 $R(x)$ 达到最小度数 $k+1$ 的 $P(x),Q(x)$ 是存在的。

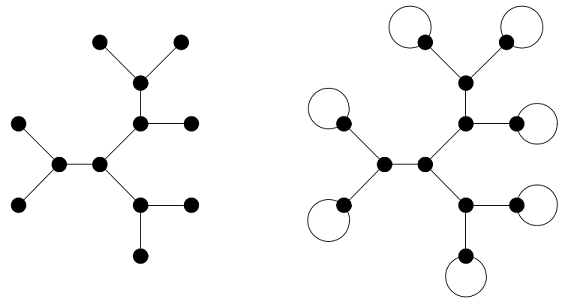
三叉树的构造，蒙 A. Zvonkine 惠允

实际上，我们可以给 $P(x),Q(x)$ 施加更复杂的限制，用同样的办法，也能得到 $R(x)$ 的最小度数。这个推广首先由 U. Zannier 在 1995 年给出，后来 A. Zvonkine 利用二部地图的方法给出了简单得多的证明。

不仅如此，根据别雷定理，二部地图和分支点只有 0、1 和 $\mathrm{\infty }$ 的分式有着一一对应的关系，所以，要知道有多少组 $P(x),Q(x)$ 能使 $R(x)$ 达到最小度数，只需要知道有多少个由 $2k$ 个顶点组成的三叉树地图。我们之前考虑 $k=5$ 的情况，截至 2000 年，数学家找到了两组解。但要知道一共多少组，只要在纸上随便画画，很容易数出来一共有四组解：

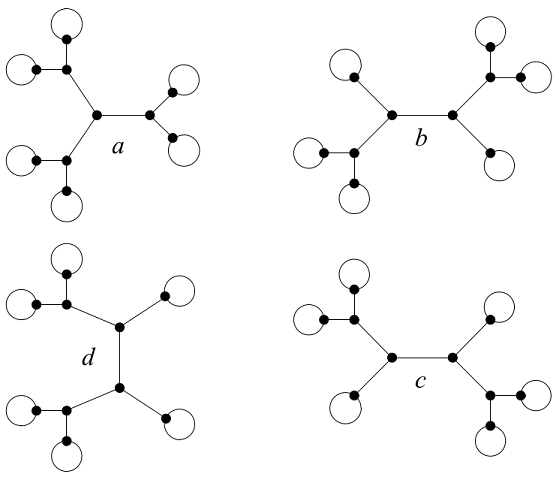
k = 5 的四组解，蒙 A. Zvonkine 惠允

通过这些地图，我们不仅能知道解的个数，还能部分推断出解的性质。树 a 和 d 各自拥有镜像对称性，所以它们对应的解的系数应该都是实数；树 b 和 c 分别是各自的镜像，所以它们对应的解的系数可能不是有理数，而是各自的复共轭。因为已知的两组解的系数都是有理数，它们对应的必定是树 a 和 d，而未知的两组解应该向复数领域寻找。果不其然，剩下的两组解在 2005 年被日本数学家盐田徹治给出，这些解的系数在 $\mathbb{Q}(\sqrt{-3})$ 中，一如预测。

这些预测又从何而来？镜像对称跟系数又有什么关系？要说清楚，就不得不提及二部地图的另一个名字——儿童涂鸦（dessin d’enfant），还有这个术语的创造者，也是现代代数几何的奠基者，伟大的数学家，亚历山大·格罗滕迪克。

一个规划的大纲

亚历山大·格罗滕迪克，图片来自上沃尔法赫数学研究所（Mathematisches Forschungsinstitut Oberwolfach）

“由于目前在大学里教学和研究方面的结合于我而言愈发虚无飘渺，我决定申请加入 CNRS，为的是能够将我的精力奉献于发展某些工作和视点，因为现在来看，明显以后找不到会代替我发展它们的学生（似乎连同行的数学家也没有）。”

（Comme la conjoncture actuelle rend de plus en plus illusoire pour moi les perspectives d’un enseignement de recherche à l’Université, je me suis résolu à demander mon admission au CNRS, pour pouvoir consacrer mon énergie à développer des travaux et perspectives dont il devient clair qu’il ne se trouvera aucun élève (ni même, semble-t-il, aucun congénère mathématicien) pour les développer à ma place.）

亚历山大·格罗滕迪克在蒙彼利埃写下这几行文字的时候，正是 1984 年的某一天，他已经 57 岁了，经历了太多太多。70 年代与嬉皮士为伍，与体制和战争展开激烈但劳而无功的抗争；60 年代在法国高等研究所日夜奋战，马不停蹄用深刻的洞察力重塑代数几何，引领法国最尖端的数学人才解决那些最难的问题；50 年代投入法国数学界温暖的怀抱，凭借高度抽象的思维崭露头角；还有颠沛流离的童年和青年时期。所有这些都已经过去了，现在他回到了他作为数学家的起点——蒙彼利埃大学——当一名教授，但他也开始厌倦教学了。

他有千言万语要说，但他也很清楚，现在面前的这几页纸，并不适合回忆。旁边厚厚的《收获与播种》（Récoltes et Semailles）的书稿，才是这些反思的去处。他现在要写的，是对今后科研的计划，直白地说，就是一份求职文件，申请的是 CNRS 的研究员职位，这可以让他免去教学的义务，专心于他的数学研究。他获得过菲尔兹奖，拒绝过克拉福德奖，这些数学界的最高荣誉，对他来说微不足道，他只要继续他的探索。

他并不喜欢体制。纳粹将他的童年破坏得支离破碎，这也许是他反体制反战争思想的来源。正是因为当年法国高等研究所接受了几笔来自军方的资助，他才愤而离开那个数学的乐园，转身投入轰轰烈烈的社会活动。现在又要回到体制，他心里大概也有些挣扎。但他决定了，即使回到体制，也要坚决拒绝腐蚀，绝对不履行那些违反良心的所谓“义务”。

但对数学真理的好奇和渴求大概根植于他心灵的更深处。当年同样的渴求让他出发重新构建了代数几何——那可是一整个数学分支——沿途还得到了无数深刻的结果。现在，他看到了一片肥沃的处女地，但却没人愿意跟他一起耕耘。他大概有些不适应。在法国高等研究所的日子里，他可是领军人物，多少人为听他一席话专程赶到巴黎郊外的 Bures-sur-Yvette，那可是一段连现在的轻轨也要花上半小时以上的小旅行。他不知道，70 年代他那些鲁莽的抗争，在一定程度上损害了他的声誉。既然没有人来做，那就只能自己来了，他大概是这样想的。

法国高等研究所，图片来自 Wikipedia

Teichmüller 层级（tour de Teichmüller）、绝对伽罗华群 $\mathrm{Gal}(\bar{\mathbb{Q}}/\mathbb{Q})$ 的作用、有限域上的正则多面体、驯顺拓扑（topologie modérée）……他笔下倾泻出近年他关心的数学领域和数学对象，这一写就是 48 页，还没算上注记。

所有这些想法，其实已经被他写在了另一份文件上，那就是《穿越伽罗华理论的长征》（La Longue Marche à Travers la Théorie de Galois）。但这份完成于 1981 年，长达 1300 页的手稿，仅仅为了他自己一个人而写，即使向别人展示，大概也没多少人会有耐心读下去吧。1300 页也许很长，但对于一直艰苦工作的格罗滕迪克来说，并不算什么。在他的黄金岁月里，有时候为了节省时间，他仅仅以香蕉和牛奶度日，终日除了休息就是研究代数几何，但这并不影响他思维的敏锐以及清晰的文笔。然而，对于求职文件而言，直接从《穿越伽罗华理论的长征》引述的话，显然不太合适。他面对的评审委员会不可能对他研究的细枝末节都了如指掌，他需要从基础说起，简洁地铺陈出他的想法。

这份求职文件，就是《一个规划的大纲》（Esquisse d’un programme）。也许数学史上再也没有别的求职文件像它那样充满真知灼见了。它很长一段时间没有被正式发表，只在数学圈子里私下流传，但它对数学的影响大概比大部分正式发表的数学论文要更大。它开创了代数几何的一个新领域，这个领域叫远阿贝尔几何（anabelian geometry）。对的，就是望月新一研究的那个远阿贝尔几何。

而对他建立这一套体系起了关键推动作用的，就是二部地图和别雷定理。所有二部地图都能给出一条对应的光滑代数曲线，但这样能否得到所有的光滑代数曲线呢？

“这样的假设当时似乎很离谱，我甚至不敢向这方面的行家询问这个问题。我问过德利涅，他也觉得确实很离谱，但手头上没有反例。不到一年之后，在赫辛斯基的国际数学家大会上，苏联数学家别雷就宣布了这个结果，他的证明简洁得不合常理，在德利涅的信里只占了两页——也许从来没有过如此深刻而奇妙的结果能用那么少的行数来证明！”

（Une telle supposition avait l’air à tel point dingue que j’étais presque gêne de la soumettre aux competences en la matière. Deligne consulté trouvait la supposition dingue en effet, mais sans
avoir un contre-exemple dans ses manches. Moins d’un an après, au Congrès International de Helsinki, le mathematicien sovietique Bielyi annonce justement ce résultat, avec une demonstration d’une simplicite deconcertante tenant en deux petites pages d’une lettre de Deligne – jamais sans doute un résultat profond et déroutant ne fut demontre en si peu de lignes!）

值得一提的是，德利涅（Deligne）是格罗滕迪克的学生，同样是菲尔兹奖获得者。在格罗滕迪克离群索居的岁月里，德利涅几乎是他获取数学新进展的唯一来源。可以看出，别雷定理给格罗滕迪克带来了多大的震动！他把别雷定理对应的二部地图称为“儿童涂鸦”（dessin d’enfant），连小朋友都能随手画出的东西，竟然蕴含着这么丰富的数学内涵！这也为他打开了一道新想法的大门：也许通过研究像组合地图这样非常简单易懂的数学对象，就能探究代数几何这门艰深学科中更深层的结构。在《一个规划的大纲》中，他探讨的就是这个可能性。

在代数数论中，所谓的“有理数的绝对伽罗华群”$\mathrm{Gal}(\bar{\mathbb{Q}}/\mathbb{Q})$ 在研究中占据了重要的地位。不要被看似复杂的符号吓倒，这就是个代号而已。可以说，代数数论中的大部分研究最终都可以跟这个群扯上关系。我们知道数学家系列：有限单群：一段百年征程，群描述的是对称性，而绝对伽罗华群 描述的则是所有代数数（也就是整系数方程的根）的对称性，它的每一个元素都是代数数集合的对称变换，惟独保持每个有理数不变。这样的对称变换又叫有理数的伽罗华变换。但到目前为止，我们仍无缘一睹这个群的全貌。对于那些“交换”（也就是满足 $ab=ba$）的部分，我们已经理解得相当透彻，但这个群的精妙之处在于它“非交换”，也就是“非阿贝尔”的部分，而我们对此仍然所知甚少。对整个绝对伽罗华群 $\mathrm{Gal}(\bar{\mathbb{Q}}/\mathbb{Q})$ 结构的研究，是代数数论以至代数几何的重要课题之一。格罗滕迪克的“远阿贝尔几何”，实际上就是尝试研究绝对伽罗华群 $\mathrm{Gal}(\bar{\mathbb{Q}}/\mathbb{Q})$ ，甚至是任意域的绝对伽罗华群，又或者更广泛的“任意代数簇的平展基本群”（étale fundamental group of algebraic varieties），它们“远离阿贝尔”的部分到底如何影响相应的代数结构的几何性质。

代数数，方程系数越小光点越大，来自 Wikipedia，原作者 Stephen J. Brooks

格罗滕迪克指出，绝对伽罗华群 $\mathrm{Gal}(\bar{\mathbb{Q}}/\mathbb{Q})$ 可以作用在所有儿童涂鸦上，因为每个儿童涂鸦对应着一个光滑代数曲线，也就是一个系数是代数数的多项式，而绝对伽罗华群 $\mathrm{Gal}(\bar{\mathbb{Q}}/\mathbb{Q})$作为代数数的对称群，当然可以通过对系数的对称变换间接作用在二部地图上。不仅如此，这个作用还是“忠实”的，也就是说，可以通过研究绝对伽罗华群 $\mathrm{Gal}(\bar{\mathbb{Q}}/\mathbb{Q})$在所有儿童涂鸦上的作用来研究这个群本身。

在绝对伽罗华群中最简单的不平凡变换就是复共轭，也就是将虚数单位 $i$ 换为 $-i$ 的变换。根据高中的数学知识，在复平面上，复共轭就是沿实数轴的镜像对称，所以它作用在儿童涂鸦上，得到的也是儿童涂鸦的镜像对称。如果一个儿童涂鸦的镜像对称还是它自己，根据别雷定理，复共轭作用到相应的代数曲线上必定得到原来的代数曲线，也就是说所有系数都是实数。如果两个儿童涂鸦互为镜像对称，它们对应的代数曲线的系数必定互为共轭，也就是说起码有一些系数是虚数。这就是我们之前猜测的理论依据。

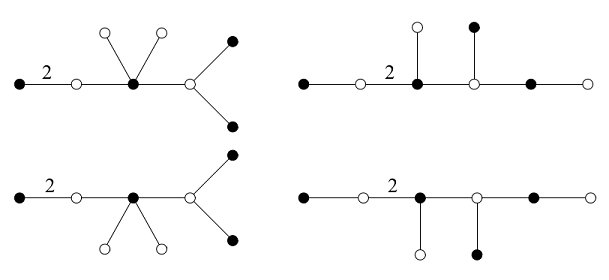
共轭对称的两个例子，蒙 A. Zvonkine 惠允

但复共轭毕竟是最简单的变换，别的对称变换的结构更为复杂。光滑代数曲线（也就是儿童涂鸦）本身有着许多对称性，对于某种对称性，有没有办法得知它是否来自绝对伽罗华群 $\mathrm{Gal}(\bar{\mathbb{Q}}/\mathbb{Q})$呢？如果能知道这一点，就相当于刻画了绝对伽罗华群 $\mathrm{Gal}(\bar{\mathbb{Q}}/\mathbb{Q})$ 本身。但这是个极端困难的问题。格罗滕迪克当时有一些初步的想法，但这远远不够。如果仅仅依靠儿童涂鸦的组合性质，就能刻画绝对伽罗华群 $\mathrm{Gal}(\bar{\mathbb{Q}}/\mathbb{Q})$ 的话，这将会震动代数几何学界：代数几何中深刻的结论，竟然可以从更简单基础的组合数学得出。

儿童涂鸦有着不少的组合不变量，它们在绝对伽罗华群 $\mathrm{Gal}(\bar{\mathbb{Q}}/\mathbb{Q})$ 的变换下保持不变：顶点个数、顶点度数、面的个数、面的度数、等等。除了这些看似简单的不变量，我们还可以给每个儿童涂鸦赋予一个群，这个群被称为“儿童涂鸦的单值群”，有时也被直接称作“地图群”。这些地图群拥有更为复杂的结构，但同样在绝对伽罗华群 $\mathrm{Gal}(\bar{\mathbb{Q}}/\mathbb{Q})$ 的变换下保持不变。格罗滕迪克的希望，就是在众多的组合不变量中能找到合适的组合，来刻画绝对伽罗华群 $\mathrm{Gal}(\bar{\mathbb{Q}}/\mathbb{Q})$。

注：然而事不如人愿。实际上，单纯的组合不变量不足以做到这一点。A. Zvonkine 举出了一个例子，说明要判断两个不同的儿童涂鸦能否通过绝对伽罗华群 $\mathrm{Gal}(\bar{\mathbb{Q}}/\mathbb{Q})$ 的作用联系在一起，有时还需要考虑一些数论方面的性质。数学家正在研究这样的情况何时会出现，原因又是什么。

但这还只是故事的开端。格罗滕迪克考虑了所谓的 Teichmüller 层级（tour de Teichmüller），它的定义非常抽象，但绝对伽罗华群 $\mathrm{Gal}(\bar{\mathbb{Q}}/\mathbb{Q})$ 同样可以作用于其上。这个 Teichmüller 层级由无穷个复杂的数学对象一层一层构成。格罗滕迪克认为，要研究有理数上的远阿贝尔几何，从 Teichmüller 层级入手可能是比较好的方法。他认为，Teichmüller 层级所有更高的部分都可以由前两层组合而来，第一层提供的是元素，第二层提供的是元素之间的关系。而这前两层恰好对应着光滑代数曲线（也就是儿童涂鸦），第二层对应的则是在数论中有着广泛应用的椭圆曲线。这就给儿童涂鸦的研究提供了充足的动机。

读到这里的读者，大概都会有一种不明觉厉的感觉。这非常正常，笔者也花了相当的时间，向不同的人请教过，才勉强捉摸到格罗滕迪克整个远阿贝尔集合计划的轮廓。格罗滕迪克写作时，文笔优美思路清晰，这份《一个规划的大纲》也不例外。但他谈论的数学实在过于抽象，难以理解。但这就是格罗滕迪克做数学的风格：尽可能从数学对象中将不必要的细节抽象出来，抽象得一般的数学家都会以为剩下的只有“虚空”，然而他仍然能从“虚空”中抓住某些东西，从而建立他的理论，完成他的证明。用格罗滕迪克本人的说法，如果把数学问题比作坚果，大部分数学家做的就是用锤子和凿子把坚果凿开，而他的做法则是将坚果浸在水里，慢慢软化它的外壳，又或者让它经受风吹日晒，然后等待合适的时机，坚果自然就会裂开。

当然坚果要放在合适的地方，否则……图片来自 Wikipedia，作者 Peter Trimming

对于大部分数学家来说，这个过程太漫长，也许只有拥有深刻洞察力的格罗滕迪克，才能在能接受的时间内，用这种方法解决问题。这也是他的数学难以被理解的原因之一：他几乎不考虑具体的示例，都是从尽可能抽象的角度出发，思考支配某个数学问题背后的宏大数学结构。有时候这也会闹出笑话。有一次讨论数学的时候，有人向格罗滕迪克提议考虑一个特定的质数作为例子。“你的意思是找一个真实的数字？”格罗滕迪克有点疑惑。对方点了点头。他回答：“好吧，我们考虑57这个质数。”57当然不是质数，但格罗滕迪克大概没有注意这一点，他从来不考虑具体的例子，一切从抽象出发。

现在，以同样的抽象风格，格罗滕迪克在《一个规划的大纲》中留下了远阿贝尔几何这一宏伟理论的框架，而儿童涂鸦在其中也占据了一席之地。他的计划，就是慢慢充实这一理论的血肉。

可惜他没有等到理论完善的那一天。

失之东隅

即使他的这份研究计划充满洞见，格罗滕迪克向 CNRS 递交的职位申请可是让 CNRS 的管理者伤透了脑筋。在职位申请的档案中，他特地写了一封信，列出了如果被 CNRS 雇用，他将会拒绝执行的一些 CNRS 雇员的义务。他的数学能力无可置疑，在 60 年代就职法国高等研究院之前他也曾经是 CNRS 的研究员（maître de recherche），但大概没有政府组织会乐意接受像他这样反体制的刺儿头。最后，在许多数学家同行的斡旋下，CNRS 以一种特殊的形式“雇用”了格罗滕迪克：他仍然保留在大学的职位，但由 CNRS 负责他的薪水。于是，他名义上还是大学教授，但因为薪水来自 CNRS，他不需要承担任何的教学义务；而又因为他名义上还是大学教授，他不需要负担 CNRS 雇员的义务。自此之后，他就越来越少踏足大学，直到四年后的 1988 年他正式退休。

在晚年，他的心灵在混乱中挣扎不休。在 1990 年，他将一些数学论文、通讯和手稿转赠给了他的学生 Malgoire，与此同时，他烧毁了大部分的与数学无关的手稿，总共大概二万五千页，全部付诸一炬。因此，我们现在无法得知他童年的具体经历。他逐渐切断了与数学界的联系，躲进了比利牛斯山脉脚下的某个小村庄，过着隐居避世的生活。而他在远阿贝尔几何上，没有什么进展。

最后，在 2014 年 11 月 13 日，他永远切断了与这个世界的联系。

比利牛斯山脉，图片来自 Wikipedia

在《一个规划的大纲》里，格罗滕迪克提出，要通过研究儿童涂鸦来研究远阿贝尔几何。但对儿童涂鸦的研究并没有预期的那么成功。有许多数学家被《一个规划的大纲》中的深邃视野所吸引，投身于儿童涂鸦的研究中，也取得了一些成果，但远远不足以达成原来的目标。

这也不是格罗滕迪克的研究计划第一次遭受挫折。早在他的黄金年代——上世纪 60 年代——他就曾提出一系列被称为“标准猜想”（standard conjectures）的猜测，实际上猜测所谓的“代数簇”背后存在某些非常深层次的算术结构。一但标准猜想被证明，许多代数数论中的猜想，例如著名的韦伊猜想（Weil’s conjectures），就能被轻松证明。实际上这也是格罗滕迪克提出标准猜想的目的。他的学生德利涅在 1973 年最终证明了最后一个韦尔猜想，但并没有取道标准猜想。德利涅想到了一个办法绕过标准猜想，使用一个更为“经典”的技巧完成了证明。而时至今天，标准猜想仍然悬而未决，也没有任何人能看到解决的曙光。

尽管与计划有所出入，远阿贝尔几何本身仍然取得了长足的进展。日本数学家望月新一在 1996 年证明了《一个规划的大纲》中格罗滕迪克提出的一个远阿贝尔几何的猜想的特殊情况，很快就闻名于数学界，还被邀请在 1998 年的国际数学家大会上作 45 分钟报告，这在数学界是一项殊荣。在积蓄了一段时间的力量后，在 2012 年，望月新一在他的个人主页上挂出了四篇文章，宣布解决了数论中一个悬而未决的重要猜想——ABC猜想。而他所用的工具，正是远阿贝尔几何，但又不单是远阿贝尔几何。

望月新一，图片来自他的学术主页 http://www.kurims.kyoto-u.ac.jp/~motizuki/top-english.html

望月新一在他的四篇文章中，基于他对远阿贝尔几何的研究，提出了一套全新的理论：宇宙际Teichmüller 几何（inter-universal Teichmüller geometry）。还记得格罗滕迪克的 Teichmüller 层级吗？望月新一的这个理论，大概就是说，考虑单一的 Teichmüller 层级还不够，需要利用某种方法，引入不同的“变体 Teichmüller 空间”（更准确地说，是“p 进制 Teichmüller 空间”的变形），再去考虑它们以及它们之间的关系，才能更好地理解整个结构。当然，实际的情况没有听起来那么简单，要定义这些数学对象，甚至要对“乘法”这样基础的数学概念进行“变形”。为了研究这些结构，望月新一还发展了许多工具，填满了四篇文章，加起来超过 500 页。

在发展这套理论时，望月新一的风格与格罗滕迪克如出一辙：将问题慢慢溶解在抽象的结构中，直到解决方法变得水到渠成。这也使他的论文格外难以理解，因为要理解他对 ABC 猜想的证明，就要先理解他的宇宙际 Teichmüller 几何，而这套理论正如其名，就像是用外星语言写就，高度抽象，根本难以入手。据说除了望月新一本人以外，目前世界上只有四名数学家看懂了证明。我们仍不知道望月新一的证明到底是对是错，但在讨论对错之前，他在远阿贝尔几何上发展的这套新理论，无疑值得赞叹。

至于儿童涂鸦，虽然它对于远阿贝尔几何研究的贡献不大，但在其他领域它却大显神通。

我们回顾一下别雷定理：每个儿童涂鸦唯一对应着一个光滑代数曲线。这是一个存在性定理：它只告诉我们对应的光滑代数曲线是存在的，但却没有具体的计算方法。许多需要具体例子的数学家对于这种“管杀不管埋”的定理颇有微词，于是他们开发出了一些具体的计算方法。这些方法现在还不能处理规模太大的儿童涂鸦，但对于许多数学家需要的例子来说绰绰有余。有了具体的计算方法，数学家就能将儿童涂鸦用于更多的数论问题上，尤其是那些与多项式相关的问题。

儿童涂鸦的另一个名字是二部地图。早在格罗滕迪克给它赋予儿童涂鸦这个名字之前，组合学家早就开始了对二部地图，以及更一般的组合地图的研究。二部地图可以推广到所谓的“星座地图”（constellation），它们对应拥有更多分支点的球面覆盖（详见参考文献中 S. Lando 和 A. Zvonkine 的著作）。对这些星座地图的研究牵涉到组合表示论、矩阵积分和弦论等高深的数学和物理分支。

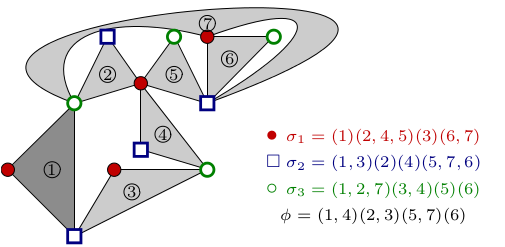
星座地图，图片由方弦制作

组合学家对于枚举二部地图（更严格地说是所谓的“有根二部地图”）也颇有兴趣，不论是球面上的二部地图，还是任意曲面上的二部地图。每个曲面都有一个叫做“亏格”（genus）的参数。球面的亏格是 0，环面的亏格是 1，然后每往曲面上多加一个“把柄”，曲面的亏格就多加 1。亏格越高的曲面，它上面的二部地图当然也越复杂。在矩阵积分的研究过程中，两位物理学家 B. Eynard 和 N. Orantin 发展了一套被称为“拓扑递归”（topological recursion）的方法，他们又发现，这套方法似乎也能用于与矩阵积分息息相关的二部地图的枚举，而且适用于任意亏格曲面上的二部地图。俄罗斯数学家 M. Kazarian 和 P. Zograf 首先将这套方法用到了儿童涂鸦的枚举上。后来，法国数学家 G. Chapuy 以及他的学生通过借用拓扑递归方法中的某些套路，证明了对于某个亏格大于1的曲面，它上面的二部地图的生成函数都能表达成一些简单函数的分式。值得一提的是，在拓扑递归方法中，最重要的一步就是计算亏格为 0 以及亏格为 1 的情况的生成函数，之后更高亏格的情况都能由这两种情况计算出来。这与格罗滕迪克对于整个 Teichmüller 层级能由最底两层产生的想法不谋而合。

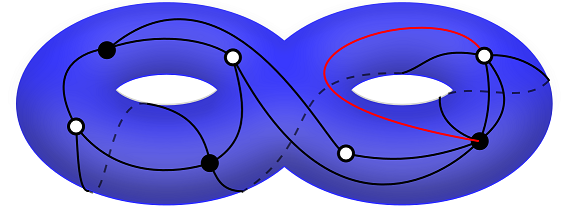
亏格为2的二部地图，由方弦制作

这就是数学的美妙之处：每个领域与别的领域之间都有着千丝万缕的联系，也许换一个视角问题就会变得深邃而重要，再换一个视角，问题又会变得无比简单。

峰回路转，柳暗花明；失之东隅，收之桑榆。这就是数学。

后记

这是一篇纪念性的文章，试验性质非常重。读到这里的读者，非常感谢你们容忍我的任性，以及所有这些不明觉厉的数学术语。这篇文章讲到的数学既简单又复杂，如果我感受到的数学之美能够向你们传递到一点点的话，我就很满足了。

我对代数几何并不熟悉。在本文写作的过程中，不愿透露姓名的金先生和欧先生给了我很大的帮助。因为他们的研究领域与代数几何相关，所以我曾多次请教他们相关的问题，而他们也很耐心地向我解释了别雷定理以及格罗滕迪克的工作，在这里要再次谢谢他们。当然，如果文章中仍然存在疏漏，那仍然是我个人才疏学浅的责任。

这篇文章的灵感来自 Alexandre Zvonkine 在波尔多的演讲《Weighted trees》。他是我所在的研究团队的一员，大家都叫他的爱称 Sacha，而他今年就要退休了，所以整个团队为他办了一场送别活动，请到了他的合作者和家属讲述他的工作和生活，《Weighted trees》就是他在送别活动上作的演讲。他高水平的演讲生动地说明了儿童涂鸦和别雷定理结合之后可以产生许多有趣的结果。这篇文章就是受他演讲的启发而写的，也用到了他幻灯片中的不少例子。我到波尔多时间不长，但也感受到他的友好。他听说我要写这么一篇文章之后，立刻问我有什么他能帮忙的，之后还关心文章什么时候写好，尽管他看不懂中文。很惭愧，跟他的演讲相比，我只做了一点微小的工作，而且还拖延了这么久。尽管有点迟，这篇文章就作为他退休之际，我送上的一点薄礼吧！

Merci beaucoup Sacha ! Bonne retraite !

Alexandre Zvonkine，图片来自他的学术主页 https://www.labri.fr/perso/zvonkin/

参考文献

Alexandre Zvonkine. Weighted trees, Journées Combinatoires de Bordeaux, 2016

Sergey Lando and Alexander Zvonkin. Graphs on surfaces and their applications, volume 141 of Encyclopaedia of Mathematical Sciences. Springer-Verlag, 2004.

Alexandre Grothendieck. Esquisse d’un programme, 1984

Allyn Jackson. Comme Appelé du Néant —— As If Summoned from the Void: The Life of Alexandre Grothendieck, Notices of the AMS, Volume 51, Number 9 and 10, 2004. Part 1, Part 2

Wenjie Fang. Aspects énumératifs et bijectifs des cartes combinatoires : généralisation, unification et application, PhD Thesis, 2016.